Q-talk 102 - Tandem Wing Airfoil Selection, Part 3
- Details
- Category: Q-Talk Articles
- Published: Wednesday, 23 December 2009 16:24
- Written by David Gall
- Hits: 3162
Thin Airfoil Theory for the Third (and Final?) Time
There are some other things about thin airfoils that are relatively consistent and insensitive to variations of camber line or thickness distribution. For one, all airfoils have a zero-lift angle of attack. That is, for each airfoil there is some angle of attack at which it will produce zero lift. For symmetrical airfoils (airfoils having a straight camber line) the zero-lift angle of attack is zero degrees. Simple enough. The angle of attack is defined as the angle between the chord line and the relative wind; for a symmetrical section at zero degrees angle of attack, the airflow is symmetrical about the top and bottom surfaces, hence, no lift is produced. If we modify that airfoil by introducing curvature into the camber line, we get a "bent trout." When a trout bends to the left, he goes left; when a camber line "bends down" it "goes down" Hmmm. What does that mean? Well, first we have to define what we mean by "bend down." If we mean bend the leading edge and trailing edge down and leave the center of the camber line arched up, we call that "positive camber." Then by analogy with a trout, the nose of the positively cambered airfoil will want to pitch down. But wait! How can there be a pitching moment if there is no lift? Ah! Two things happen:
First, when we bend the camber line, even at zero degrees angle of attack, the airfoil will now make lift! Thus, there is a lift force that can make a pitching moment about the aerodynamic center and the airfoil will "go down" - er, pitch nose down. So now, if we want to find the zero lift angle of attack, we must pitch the nose down even more, implying that whatever the number is for the zero lift angle of attack for our airfoil, it will be a negative number. Don't let this throw you. Remember, since the zero lift angle of attack is a negative number, and the airfoil does make lift at zero degrees angle of attack, it is entirely possible that the angle of incidence you'll want to use to attach the wing to the airplane may also be a negative number, somewhere between the zero lift angle of attack and zero degrees angle of attack. That's okay! Some airplanes are meant to be built that way. To illustrate further: The cambered airfoil still has a zero-lift angle of attack just like the symmetrical airfoil, it just doesn't happen at zero degrees angle of attack. In fact, as anyone who's ever flown inverted in a Citabria or similar can attest, the lift can actually "go negative" or pull toward the bottom surface of the wing, even though the wing is positively cambered, so there must be some "crossover" point where the lift is zero as it goes from positive to negative. Indeed, there is a zero-lift angle of attack somewhere in the negative angle of attack range, typically about minus-two to minus-five degrees angle of attack for common general aviation airfoils.
Second, the pitching moment of cambered airfoils is always present. It never goes to zero as it does for symmetrical airfoils. Specifically, the pitching moment of cambered airfoils does not go to zero at the zero-lift angle of attack. No, cambered airfoils continue to make pitching moments even when making no lift. Imagine that the front part of the airfoil is a smaller airfoil all to itself, and the back part likewise, and you'll see that the two parts are set at an angle to one another like the nose and tail of a "bent trout" and that makes the nose part pull one way and the tail part pull the other way, no matter what the overall airfoil angle of attack maybe.
Recapitulation - Control Surfaces
When we last looked at longitudinal balance, we left off saying that we would need to discover the aerodynamic center. We have and along the way we've discovered some common properties shared by all modern airfoils. Before we return to longitudinal balance, let's recap what we know about airfoils:
1. Symmetrical airfoils have straight camber lines (zero camber).
2. Symmetrical airfoils make zero lift at zero angle of attack.
3. Symmetrical airfoils make zero pitching moment.
4. Cambered airfoils have curved or "arched" camber lines.
5. Cambered airfoils make zero lift at a small negative angle of attack.
6. Cambered airfoils make negative (nose-down) pitching moment.
7. All airfoils make lift coefficient in proportion to angle of attack, within limits.
8. All airfoils have a limiting angle of attack beyond which they stall.
9. When stalled, lift coefficient no longer varies in proportion to angle of attack.
10. When stalled, pitching moment coefficient is no longer nearly constant.
If we add a trailing edge flap to an airfoil and deflect its trailing edge down, we effectively increase the airfoil's camber. Many people think that we also increase its angle of attack when we do so, but, by definition, the angle of attack is the angle between the relative wind and the chord line of the original airfoil. So what we get is an airfoil operating at a "real" angle of attack that is larger than what we report for its angle of attack.
In other words, if we were to respect the definition of the chord line as extending from the leading edge to the trailing edge, we would acknowledge that the extension of the flap did, in fact, increase the angle of attack. However, we suppress that in favor of retaining the original chord line as our angle of attack reference line. This has its purpose in studying airplanes wherein we decide to permanently bolt the wings to the fuselage and suddenly find that the bookkeeping required by a constantly shifting chord line is too much to keep up with. Better to choose one chord line and live with the apparent contradiction.
Because of this, we find that the stall angle of attack of a wing with the flaps down is "less" than with the flaps up, even though the (maximum) coefficient of lift generated at the stall is higher. But is the "real" angle of attack the same, smaller, or larger? That question, it turns out, is immaterial. We simply don't care. We can certainly find out, if we need to. However, we do note that with a flap extended, an airfoil is modified from its original form to have a greater amount of camber. And we already know that more camber means greater lift coefficients at all ("real") angles of attack and a more-negative zero-lift angle of attack.
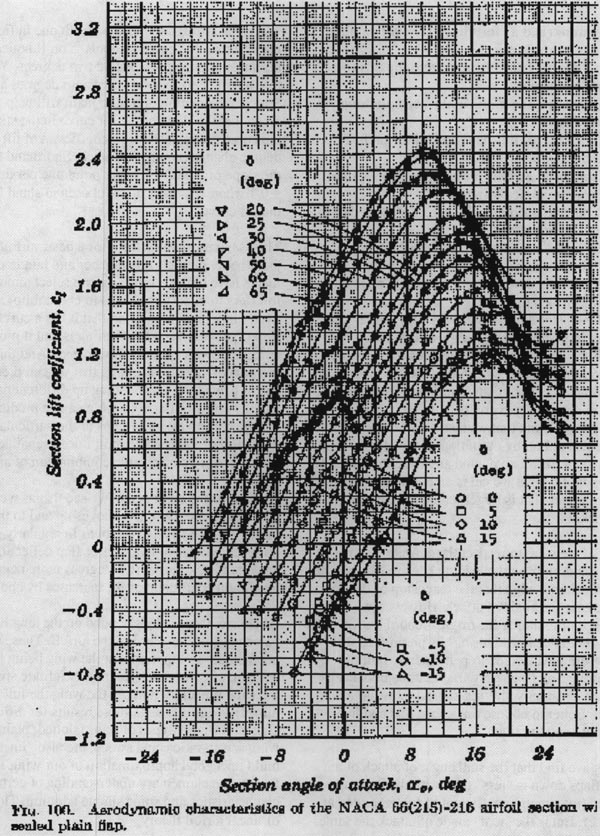
This is shown graphically in the following chart for a "typical" NACA airfoil. Notice that, as the flap is deflected more, the same basic curve-shape moves up and to the left on the chart. Don't be afraid to spend time with a chart such as this; I've spent a good half hour looking at it and I already know what I'm looking for.
The basic airfoil curve is the fourth one in from the right, marked with the circle symbols. You'll notice that its zero-lift angle of attack is negative two degrees. You'll also note that its lift coefficient is 0.2 at zero degrees angle of attack. Simple observation or a little math will help you to conclude that the slope of the lift curve in the straight part of the curve gives a change in coefficient of lift of 0.1 for each degree change of angle of attack. Shorthand for this is that the slope of the lift curve is "point one per degree" or just a = 0.1 where a is the symbol chosen to stand for the slope of the lift curve.
This is a typical value for a for a basic airfoil section. In fact, theory predicts this number and hundreds of experiments have borne it out. You can select almost any thin airfoil (less than 20% thickness to chord ratio) and look at its wind tunnel report and find that it has a curve with the same slope. The beauty of this finding is that it proves that thin airfoil theory is substantially correct. And thin airfoil theory is a "linear" theory, meaning that we can predict changes in airfoil behavior by just adding up different parts. For example, the effect of flap extension can be predicted by just adding the generic effect of flaps to the particular lift curve of the airfoil of interest. We don't need separate wind tunnel tests for every conceivable combination of airfoil and flap!
Looking at the chart again, we see that as we deflect the flap more and more, the curve moves up and to the left more and more. We also see that it moves in regularly spaced steps. For each additional five-degree flap deflection, the zero-lift angle of attack moves two degrees more negative and the maximum coefficient of lift increases by about 0 .1.
Of course, these values depend on the length of the flap as a percentage of the chord of the airfoil. These values also depend on the assumption that the wing being tested is straight, of constant chord, and of infinite span (simulated in the wind tunnel by running the wing the full width of the tunnel). Adjustments to these results for different flaps chords, different types of flaps (slotted, plain, etc.), different wing aspect ratios, and sweep, are also "linear" so we can build up a good approximation of our wing's behavior just from some elementary understanding of certain general characteristics and some simple addition. This is the essence of linear airfoil theory.
In fact, linear airfoil theory is so powerful that we now can replace our airfoils by simple straight lines. These lines serve as placeholders for the future placement of particular airfoils whose characteristics we will specify during the design process. In order to take this final step to eliminating the particular airfoil shape in favor of a generic placeholder, we must do one more thing. We must find a common reference line that is generic to all airfoils. As noted previously, each airfoil has an angle of attack at which it develops zero lift. If we draw a line on the airfoil to represent the direction of the relative wind at this zero lift angle of attack, and if we draw this line so that it goes through the trailing edge of the airfoil, we can call this line the Zero Lift Line orZLL.
Further, if we measure angle of attack to this line instead of the airfoil chord line, then we will always be able to specify later the location of the chord line of the particular airfoil that we eventually choose. Additionally, we will always know a positive angle of attack measured to this line will mean that we are making lift; we call this new angle the "absolute angle of attack" and give it the symbol aa. We now have all the tools in place to discuss the requirements that our design imposes on our airfoil selection without needing to consider specific airfoils in the discussion.
So, why is there so much hoopla over different airfoils if they all behave so much alike? Well, the lift curves are all pretty much alike, but the drag curves and the moment curves are different. The drag curves come in two varieties, tuibulent-flow and laminar-flow, but they all have pretty much the same shape. We won't spend any time on drag curves; there's still too much other material to cover. Moment curves are more important to our interest right now, but, as noted previously, they are pretty boring! As long as the airfoil is not stalled, the coefficient of moment is generally constant, or nearly so. We'll treat it as constant for discussion purposes. The important feature of moment curves in airfoil comparisons is the value of that constant moment coefficient from one airfoil to the next. And, later, we'll see that the differing value of the moment coefficient at varying control surface deflections is also very important.
Stability and Control
Now we have enough parts of the picture to finally look at longitudinal
balance. As preamble, lets outline a road map of the topics to be examined for stability and control. First, we're going to limit ourselves to longitudinal stability and control. There will be no discussions of lateral or directional stability or control. Further, within longitudinal stability and control we will almost completely ignore control. There is just too
much to discuss about things such as elevator floating angles and control stick forces. We will simply assume that these issues do not present a problem in context to our discussions and can be dealt with after-the-fact. I don't want to de-emphasize the importance of such issues; they are simply beyond the scope of this article.
Thus, we're left to discuss longitudinal stability. Stability is broken down into dynamic stability, which cannot exist in the absence of positive static stability, and static stability which cannot exist without first having longitudinal balance. We won't discuss dynamic stability. We take it for granted that the dynamic stability of our creation will be adequate. In the areas of both static and dynamic stability there are two cases to be examined called "stick-fixed" and "stick-free" depending on whether we expect our test pilot to hold the control stick firmly or let it go. Again, we won't discuss the stick-free case in the interest of brevity(!) except to occasionally mention that we need to make sure that the airplane can be trimmed for a given condition, and then to assume such is possible.
Finally, we've whittled our scope down to the narrow topic of stick-fixed longitudinal static stability. That topic, in turn, requires the establishment that the airplane be longitudinally balanced.
Next Time: Longitudinal Balance Continued
You can order a printed copy of Q-talk #102 by using the Q-talk Back Issue Order Page.



